—
 |
| Кот Ольги… |
—
Данная глава посвящена внутренним параметрам точек и правилам создания живых существ (их поведения, реакций на раздражитель и прочее). Это собственные значения живого существа (или его разновидности), с которыми оно существует в этом мире. Внутренние параметры задаются принудительно, это настройка существования живого существа.
—
В теории математическая точка движется от самой себя (имеет другое будущее относительно себя в прошлом) к другой точке или от нее, что увеличивает или уменьшает величину раздражения (расстояние между точками). Но ради такого примитива едва ли стоило затевать столь сложную технику, как живое существо, поэтому на практике все устроено сложнее. Когда мы говорим о технике, то должны иметь ввиду, что у нас есть механизм изменения какого-то параметра, что и является смыслом психологии. Если у нас есть вентилятор, но нет механизма управления скоростью вращения лопастей, то не будет и психологии в виде раздражения и реакции на раздражения. Но если такой механизм есть, то начинается психология, которая сводится к управлению каким-то параметром в зависимости от входящих данных (внешней среды). Для примера в качестве входящей информации мы возьмем температуру, это раздражитель для нашего вентилятора. Вращение лопастей (двигателя) — это реакция на раздражение. Для живого существа все немного иначе, так как регулирование параметра происходит через химические реакции, но математический и геометрический смысл такой же, поэтому для простоты и удобства остановимся на примере температуры и скорости вращения.
Величина реакции находится в зависимости от величины раздражения. Зависимость может быть какой угодно, прямой (чем выше разница температур, тем выше скорость вращения), обратной (чем выше разница температур, тем ниже скорость вращения), линейной (скорость вращения линейна разнице температур), какой-то еще (скорость вращения находится в зависимости от разницы температур по какой-то замысловатой функции). Но величина раздражения всегда как-то соответствует величине реакции, а тип (имя или адрес) раздражения типу (имени или адресу) реакции. Как именно и что именно — это прихоть разработчика живого существа (или его аналога в виде управления вращением вентилятора). Это может быть величина подачи газа в зависимости от величины освещения, величина громкости крика от ужаса в зависимости от величины подачи газа, степень ужаса в зависимости от расстояния до источника ужаса и так далее. Для простоты и удобства мы остановимся на прямой и линейной зависимости величины вращения от величины разницы температур. Это значит, что один градус соответствует одному обороту в минуту. Когда мы определились с соответствием размерности величин (потому что в психологии они могут соответствовать друг другу как угодно), то мы должны определиться с внутренними параметрами и их соответствием.
 |
| Это стандартная математическая точка. Почти, нам еще ее предстоит создать. Создание математической точки начинается с создания ассоциированного пространства, в которое будет проводиться возбуждение. Ассоциация создается по правилам преобразования величин, в данном случае температуры ассоциированы со скоростью вращения, логику пропустим, одно пространство соответствует другому один к одному. Это значит, что один градус температуры равен одному обороту в минуту. И пусть это будет линейная зависимость, на увеличение разницы температур наша точка реагирует увеличением скорости вращения. |
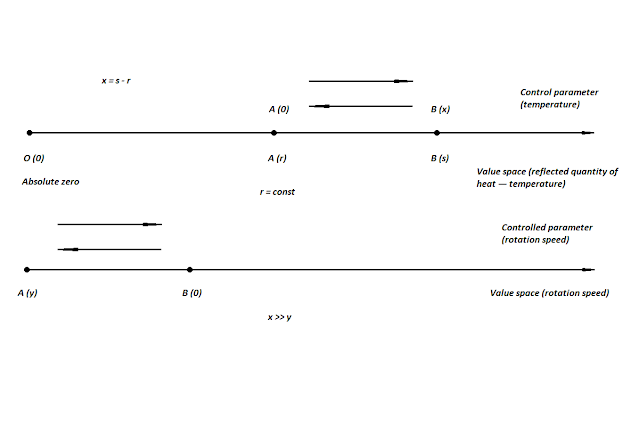
Внутренний параметр — это некоторая внутренняя величина точки. Она не является действительно существующей и задается принудительно. На прямую наносится одна точка, которая в психологии далее считается началом координат. Она делит прямую на две области одномерного пространства, это относительный ноль, который может находиться на некотором расстоянии от абсолютного нуля. Длина такого отрезка относительно абсолютного нуля — это и есть внутренняя величина. Разница температур возникает относительно этой точки, как и разница оборотов двигателя. Математическая точка виртуальна, она не может двигаться в одномерном пространстве, как это делают действительно существующие точки. Но если мы имитируем энергетическое взаимодействие, то можем имитировать и движение точки, которое происходит при настоящем энергетическом взаимодействии, для чего нам и нужна вычислительная мощность. Разумеется, что мы не собираемся виртуально перемещать точку в этом же пространстве, это глупо и скучно. Никто не запрещает, но вообще-то это происходит автоматически в окружающей действительности и без психологии, мы собираемся имитировать окружающую действительность и ее закономерности (но с учетом таких закономерностей). В целом, положение такой точки всегда константа, оно отражает нам величину одного из потенциалов и состояние покоя как отсутствие раздражения и реакции на раздражение (отсутствие разницы потенциалов), потому что такая точка не может образовать отрезок сама с собой в актуальном настоящем. Для нашего примера с температурами это внутренняя температура точки, которую мы считаем заданной. Мы можем задать ее величину равной абсолютному нулю, но это в нашей действительности глупо и холодно, поэтому мы будет считать, что она больше нуля и равна некоторой величине (r) или длине OA.
 |
| У нас есть некоторая математическая точка на прямой с внутренним виртуальным значением (r) относительно абсолютного нуля. Это значит, что она отражает некоторую заданную температуру. Единицы отражения могут быть разные (разная шкала), пусть это будут шкала Кельвина (K). Этому значению соответствует некоторое значение скорости вращения. Будем считать, что оно равно нулю (отсутствие вращения). |
Математическая точка должна присутствовать и на прямой, которая отражает совершаемую работу, это точка пересечения двух пространств. Если не установить положение точки в ассоциированном пространстве, то не будет ответа на вопрос, относительно чего должна увеличиваться частота вращения. Для простоты и удобства мы договорились о прямой и линейной зависимости величины вращения от величины разницы температур. В данном примере пока еще нет разницы температур, поэтому нет величины вращения. Но никто не мешает нам установить заданную величину вращения, отличную от нуля. В этом случае вентилятор будет крутиться с некоторой частотой. Это та частота вращения, которая соответствует температуре (r) — состоянию покоя. Это тоже внутренний параметр точки. И нас не должно пугать, если в состоянии покоя (отсутствия раздражителя) двигатель будет наматывать обороты, это тоже нормально. В состоянии покоя у живого существа есть множество параметров, чья величина отлична от нуля (пульс и частота биения сердца, например). Но для простоты и удобства мы будем считать, что в состоянии покоя двигатель не крутится. Таким образом, у нашей математической точки есть два внутренних параметра, которые соответствуют друг другу. В нашем примере некоторая температура (r) соответствует отсутствию оборотов двигателя. И есть два пространства значений, которые тоже соответствуют друг другу (один градус Кельвина соответствует одному обороту двигателя).
—
Мы помним о том, что тело удерживается в состоянии покоя, пока нет силы, которая принудит его выйти из этого состояния. В состоянии покоя наш вентилятор не будет работать (или будет работать с той частотой, которую мы задали). Точка находится в состоянии покоя, пока нет второй точки, с которой можно образовать отрезок прямой (входящее определение), и которая самим фактом вынудит точку изменить свое состояние покоя (прийти в какое-то движение). Это значит, что она механически переносит свою позицию из прошлого в будущее без изменения (прошлое симметрично будущему). Но вот наконец-то появляется раздражитель, с которым можно образовать пару (создать отрезок прямой). Будем считать, что точка нагружена контрольно-измерительным прибором (органом чувств), который возвращает ей величину, а не логическое истинно (т.е. некоторую измеренную длину отрезка прямой, а не просто информацию, что другая точка нашлась).
 |
| Появление второго конца отрезка прямой сообщило математической точке, что она существует, и как именно существует. Отрезок AB (или координата (х)) — это определение точки, в данном случае разница температур. Если иначе, это разница значений AB = OB – OA (x = s – r). Данная величина является действительно отраженной, она отражает физически существующую разницу количества теплоты и используется вместо импульса (разницы масс и скоростей в механике). Далее положение точки B отражается в другое пространство (исходящее определение) по правилам преобразования величин, двигатель отреагировал на появления раздражителя пропорционально его величине (x >> y). |
Контрольно-измерительный орган чувств точки что-то измерил в градусах Кельвина. Мы договорились, что они соответствуют числу оборотов один к одному (х >> у), поэтому величина реакции равна величине раздражителя. Это значит, что наш пропеллер начал крутиться с частотой, которая равна разнице значений (температур). Это пусть и примитивная, но достаточно понятная иллюстрация того, как происходят реакции на раздражитель у живого существа. Величины пропорциональны, чем выше разница температур, тем быстрее будет работать двигатель, и наоборот.
—
Что произойдет, если мы не установим соответствие двух пространств между собой? Во-первых, наше живое существо, которое реагирует на разницу температур своим пропеллером, попросту не будет понимать, что на изменение температуры (то, что измеряет градусник) нужно реагировать вращением пропеллера, т.к. мы не установили соответствие имен. Во-вторых, если имена соответствуют, но не установлено соответствие величин, то и в этом случае наше живое существо не будет понимать, как именно оно должно реагировать на изменение температуры. Градусник вернул что-то в Кельвинах, есть разница температур, но живое существо не знает, сколько это в оборотах в минуту. Логика в таком случае задается по умолчанию, если есть разница температур, то есть соответствующая частота вращения. Это единственное, что можно установить по желанию, но все остальное нужно установить, чтобы это просто работало.
Что произойдет, если мы установим соответствие пространств, но не установим положение математической точки в ассоциированных пространствах? Во-первых, наше живое существо не будет знать разницы температур относительно себя, потому что градусник возвращает значение относительно абсолютного нуля. В этом случае точка не будет являться субъектом, у которого есть собственная температура (пусть и виртуальная). Поэтому оно не будет знать величины раздражения, или будет считать таковой температуру, которую измерил градусник. Во-вторых, наше живое существо не сможет увеличить число оборотов, потому что не знает, относительно чего нужно увеличить число оборотов. Поэтому оно не сможет дать нужную величину реакции в виде увеличения частоты вращения. И третье, если мы не установим соответствие положения точки в обоих пространствах, то пространства окажутся разорванными, даже если мы их ассоциировали, потому что математическая точка находится на пересечении двух пространств. Такое положение является началом координат в обоих пространствах и состоянием покоя (когда величины температуры и вращения двигателя следует считать нормой, потому что раздражитель задает отклонение от нормы).
Что произойдет, если в соответствие состоянию покоя мы поставим другую величину вращения, отличную от нуля? В этом случае наш вентилятор станет крутиться быстрее относительно себя (этой величины) на величину, пропорциональную величине раздражителя. Без раздражителя он должен крутиться с той частотой, которая установлена как состояние покоя. Если мы изменим соответствие величин с прямого (x = y) на какое-то другое (например, x = 2y), то в этом случае наш вентилятор будет крутиться в два раза быстрее при той же разнице температур, что и раньше. А если определение и реакция будут соответствовать как (x = y^2), то мы расстанемся с линейной зависимостью, и до максимальных оборотов двигатель раскрутится даже при незначительной разнице температур. И так далее.
Но мы всегда должны объявить соответствие размерности величин (какому количеству оборотов соответствует один градус Кельвина в нашем примере) и соответствие их позиций (какой величине внутреннего параметра определения в состоянии покоя (отсутствия раздражителя) соответствует управляемый параметр совершаемой работы в состоянии покоя). Это базовое правило создания живых существ, что должен знать и во что должен уметь каждый психолог, если это психолог. Только в розовых фантазиях есть эволюция, где такое соответствие может появиться само по себе, а не на стадии проектирования живого существа. В нашем примере величина частоты оборотов в состоянии покоя равна нулю, но может быть и не равна нулю. А еще у живого существа есть частота биения сердца, которая тоже может меняться (увеличиваться) при раздражении, и в состоянии покоя ее величина отлична от нуля. Еще у живого существа есть величина концентрации в крови чего-нибудь, которая тоже меняется пропорционально раздражению, есть мышечное напряжение, которое должно быть адекватно величине раздражителя, иначе живое существо может не успеть убежать в случае опасности. И так далее. Если что-то будет неадекватно соответствовать другому (или вообще не соответствовать), то живое существо может сдохнуть, едва родившись (или вообще не родившись).
—
Теперь немного поиграемся с нашей моделью. Предположим, что совершаемая работу в состоянии покоя не равна нулю, это некоторая величина. Ей соответствует некоторая температура, которая тоже не равна нулю относительно абсолютного нуля. Если градусник возвращает значение больше внутреннего значения нашего живого существа, то это команда (инструкция) увеличить на соответствующее количество обороты пропеллера. А если меньше? Формально в этом случае наше живое существо должно отреагировать снижением количества оборотов. И на этом месте врывается практика, которая, возможно, объясняет modus operandi разработчиков всего живого. Когда совершаемая работа в состоянии покоя равна нулю, то возвращаемые отрицательные значения (меньше относительного нуля — это внутренняя температура нашего живого существа) не могут вызывать реакции, потому что двигатель не может снизить частоту вращения в отрицательную величину, наше живое существо просто не будет реагировать на температуры ниже заданной. Но если нулевая частота не равна нулю, то вроде бы может. В этом случае это будет команда (инструкция) присвоить себе значение, которое ниже относительного нуля, но все еще выше абсолютного нуля.
 |
| Положение точки B проецируется (отражается) из одного пространства в другое. Если обе прямые направлены одинаково слева направо (A (r) >> A (n)), то положение слева соответствует и в работе положению слева, т.е. это команда (инструкция) снизить количество оборотов со значения (n) до значения (m). Увы, но так это не работает. |
Если отрезок ОА на первой прямой больше отрезка ОА на второй прямой, и отрезок AB на первой прямой окажется больше отрезка OA на второй прямой, то мы снова увидим отсутствие реакции на раздражитель, потому что абсолютный ноль на второй прямой — это выключенный двигатель. Мы сталкиваемся с тем же, с чем сталкивались в определениях, что помимо относительного нуля, который может быть где угодно, есть реальность, в которой ноль — это ноль. Да, наш двигатель может снизить частоту вращения ниже относительного нуля (частоты покоя), но ее нельзя снижать до бесконечности. Поэтому для направления справа налево придется устанавливать другое соответствие, даже если наш градусник может вернуть значение ниже установленного как ноль. Так у нас появляются пространства за спиной как на одной прямой, так и на другой. Это значит, что две прямые соответствуют друг другу только до положения математической точки (или только от положения математической точки). Если мы хотим, чтобы температура ниже относительного нуля (внутренней температуры) тоже была раздражителем, то для нее нужно настроить свое соответствие, свою реакцию (и это необязательно снижение оборотов двигателя, это может быть тоже увеличение оборотов, или вообще какая-то другая реакция, например, сирену включить) и может быть даже свой контрольно-измерительный прибор, который измеряет в другую сторону.
 |
| Это еще одна вариация, раздражитель слева, работа справа. Это значит, что при понижении температуры ниже установленной будет вращаться пропеллер. Чем больше разница температур, тем больше оборотов. |
Получаются всего четыре варианта. С первым мы знакомы, это (A (r) >> A (n)), оба пространства направлены в одну сторону. Чем более горячим является измеряемое тело, тем сильнее крутится пропеллер. На картинке другой вариант, (– A (r) >> A (n)), направления пространств противоположны. Это значит, что величина раздражителя будет меньше условного нуля, но работа будет совершаться в положительную сторону, т.е. чем более холодным является измеряемое тело, тем сильнее крутится пропеллер. Все может произойти точно так же, но в другую сторону, (A (r) >> – A (n)), чем более горячим является измеряемое тело, тем меньше частота вращения относительно условно нулевой. У такого варианта появляется недостаток, температура измеряемого тела с некоторого момента станет соответствовать выключенному двигателю, т.е. отсутствую реакции на раздражитель, поэтому такие варианты требуют отдельной настройки. Они применяются часто, например, вести себя как можно тише в момент опасности, что соответствует понижению совершаемой работы. И последний вариант, это совпадение направлений в сторону абсолютного нуля (– A (r) >> – A (n)). К пределу совершаемой работы (выключенному двигателю) добавляется предел измерения (свойство не выражено). Такие варианты требуют еще более ювелирной настройки, потому что не только некоторая температура может выключить двигатель, но и некоторая работа двигателя может выключить температуру. Живое существо от такого сдохнет раньше, но все-таки. Чем более холодным будет измеряемое тело, тем меньше совершаемой работы (частота вращения двигателя в нашем случае). Вполне возможно, что именно такие особенности являются причиной столь странной аналитической геометрии, потому что тогда она вполне рациональна, потому что диктуется необходимостью (с этим мы еще столкнемся и далее), но может быть есть и другие причины. Но в данном случае мы можем наблюдать аналитическую геометрию во всей красе. Математическая точка является всегда входящей при определении (раздражитель исходящая), при работе она вроде бы всегда исходящая, потому что меняет координату. Но если посмотреть глазами внешнего наблюдателя, то она и в пространстве работы не опускается ниже какого-то установленного положения, т.е. в какой-то степени является входящей. Ну и конечно принцип, что две точки при любом положении смотрят друг на друга, т.к. математическая точка не может убежать дальше раздражителя.
—
Продолжим играться с нашей моделью. Управляющее и управляемое значение никак не связаны, величина раздражения просто задает величину реакции. Если считать условный ноль точкой равновесия, то любое раздражение — это величина неравновесия. Но это не единственное, что может быть. Количество теплоты, как физический феномен, тоже как-то соответствует температуре через преобразование величин. Если учесть, сколько разных способов измерения существует (градусы Кельвина, Цельсия, Фаренгейта, можно придумать свою шкалу), то варианты преобразования количества физического явления в определение (цифру) тоже могут быть самые разные, а значит и итоговая величина определения. Математическая точка виртуальна, поэтому у нее не может быть собственной температуры, она не существует физически, но физически существует материальный носитель математической точки (как физический процессор является носителем виртуальной операционной системы), материальная точка способна вступать в физические взаимодействия, в нашем случае нагреваться или остывать относительно себя в прошлом. Математическая точка может образовать отрезок прямой со своей физической оболочкой, насколько температура носителя отклонилась от заданной (виртуальной). Наш контрольно-измерительный орган чувств измеряет разницу температур между внутренней температурой точки (заданной константой) и окружающей среды в положительную сторону (больше внутреннего значения точки). Носитель — это тоже часть окружающей среды, он может нагреваться, потому что материальные точки тоже могут проводить возбуждение. Они проводят его согласно второму закону термодинамики, выравнивая свои значения, поэтому внутренняя температура (виртуальная) и собственная температура градусника — это разные вещи. В реальности каждое живое существо сверяет собственную температуру (тела, какая она есть) с внутренней температурой (какой она должна быть), и любое отклонение — это уже образование полноценной математической точки и какого-то раздражения (реакции организма на повышение или понижение собственной температуры относительно внутренней). Это еще один смысл психологии — контроль параметра и отклонений от заданного параметра (величины отклонений).
 |
| Это пример такого контроля, чем больше разница температур между значением математической точки и значением измеряемого объекта, тем выше работа охладителя, которых охлаждает измеряемый объект, тем ниже его работа, тем меньше работа охлаждения, тем выше разница температур и так далее. Математическая точка не может образовать отрезок прямой сама с собой в актуальном настоящем, поэтому ее температуру (относительно абсолютного нуля) нужно задать. Температура B — это температура чего угодно, в том числе и носителя математической точки (тела, мозга, микросхемы и так далее) относительно абсолютного нуля. Отрезок прямой между математической точкой и раздражителем — это разница температур между той, которая должна быть и фактической. Разница значений соответствует некоторому количеству раздражения (в нашем случае разнице температур). Соответственно, любое раздражение — это отклонение фактической температуры от заданной. |
Охлаждаемое тело не будет остывать сразу, равно как и сразу нагреваться при отсутствии охлаждения, поэтому работа вентилятора (или другого охладителя) будет носить волнообразный характер, туда или сюда (быстрее или медленнее). Но у такой волны будут пики, выше или ниже которых охлаждаемое тело не нагреется и не остынет, равно как будут пики работы и у вентилятора, выше или ниже которых не поднимется и не упадет частота вращения. Это пример искусственной зависимости, когда величина раздражения контролируется через реакцию на раздражение с целью ее уменьшить. Волнообразной работа здесь будет исключительно из-за некоторого отрезка времени, которое нужно телу, чтобы нагреться или остыть. Если тело будет остывать и нагреваться сразу, то частота вращения двигателя застынет пропорционально застывшей средней разнице температур.
Аналогичным такому примеру будет поведение живого существа, которое убегает от раздражителя, тем самым снижая величину раздражения, потому что чем дальше, тем менее страшно. На некотором расстоянии скорость движения упадет до нуля (состояния покоя), потому что уже далеко. Аналогично и для концентрации чего-либо в организме, если концентрация превысила установленную норму, то реакцией на раздражитель становится работа, которая приведет концентрацию в норму (если живое существо от этого не сдохнет). Аналогично контролируется температура тела живого существа, при повышении температуры возникает определенность для математической точки, значит пора повысить концентрацию чего-нибудь, чтобы привести температуру в норму и так далее. Эти примеры объединяет одно — работа, вызываемая неравновесием (дистанцией между математической точкой и раздражителем) направлена на достижение равновесия (сократить такую дистанцию до нуля), чтобы параметр таким образом вернулся в состояние покоя (относительного нуля). Если совсем грубо, то разбить лицо раздражителю, чтобы больше не раздражал. Поведение не сводится только к этому, но это настолько часто встречающийся прием, что можно сказать, что каждое живое существо в своих действиях стремится к состоянию покоя (ничего не делать). В том числе и почесаться, чтобы не чесалось, еще один пример работы, направленной на уменьшение раздражения.
Впрочем, даже это требует некоторой настройки. Если разница температур будет постоянной, то постоянной будет совершаемая работа. Это будет новым состоянием покоя для вентилятора, которое отлично от состояния покоя, когда математическая точка не определена (нет раздражителя как второго конца отрезка прямой), но тоже неизменно, потому что тело (управляемый параметр) удерживается в состоянии покоя, пока нет силы, которая принудит его выйти из этого состояния, т.е. пока не изменится величина разницы значений между внутренним параметром и тем, что измерил контрольно-измерительный градусник (орган чувств). Другими словами, если работа, которая направлена на раздражитель, не приводит к сокращению дистанции до нуля, а к некоторой застывшей разнице, то и работа станет застывшей. Постоянная боль, постоянная повышенная температура, постоянные дебилы, которые мешают жить, еще что-то постоянное, потому что величины реакции недостаточно, чтобы умножить величину раздражения на ноль. Например, организм не справляется с тем, чтобы вернуть какой-то параметр в состояние покоя, из-за чего есть целая индустрия лекарственных препаратов.
—
Дальнейшая игра с моделью — это настройка соответствия определения и совершаемой работы через количество раздражения и количество возбуждения. До этого момента подразумевалось, что величина определения задает величину совершаемой работы. И если есть отклонение от заданного параметра в пространстве определения, то должно быть соответствующее отклонение от заданного параметра в пространстве совершаемой работы. В нашем случае это была температура и вращение лопастей, но в психологии это работает немного не так. Они соответствуют друг другу не напрямую, а через буферное математическое пространство, где определение переводится в раздражение, раздражение в возбуждение, а возбуждение в совершаемую работу. Поэтому дальнейшая настройка — это настройка величин, какому количеству раздражения соответствует одна единица определения (в нашем случае один градус Кельвина), и какой совершаемой работе (в нашем случае частоте вращения) соответствует одна единица возбуждения. Но так как возбуждение — это часть раздражения, проводимое в совершаемую работу, то мы ограничимся самим раздражением, изменение координаты можно считать и так тоже.
Соответствовать они могут как угодно, в том числе и один к одному. Но для этого тоже не обязательно конструировать такое сложное изделие как живое существо, поэтому обычно они соответствуют друг другу достаточно замысловато. В том числе и потому, что многие действительные определения отражаются абстрактно, и только после этого отражаются еще раз как величина раздражения. Но и без абстрактных отражений вариантов море. Например, количество раздражения может соответствовать квадрату определения. Смысла в этом немного, потому что определение задает длину отрезка прямой в математическом пространстве, не более. В качестве примера мы брали температуру тела, которую можно перенести в математическое пространство один к одному. Можно перенести как квадрат, в этом случае увеличение длины отрезка в определении будет увеличивать во второй степени длину отрезка в математическом пространстве. Если мы отражаем определение абстрактно, то (для примера) длина отрезка (определения) сначала соответствует какой-то длине отрезка опасности, чем больше разница температур, тем опаснее для нашего живого существа (сгорит и сдохнет). И после этого величина опасности переводится в величину раздражения.
 |
| В психологии количество раздражения (длина отрезка в математической реальности) всегда находится в зависимости от входящего определения (если оно не вызывается из памяти, это длина отрезка в физической реальности), чтобы живое существо взаимодействовало с физической реальностью. Это пример такой зависимости, когда количество раздражения равно квадрату определения. Если речь идет о температурах, то можно представить себе разницу температур, возвести ее во вторую степень и оценить величину раздражения. И чем дальше будет точка B, тем больше будет количество раздражения уже совсем не линейно. Смысла в этом никакого, мы просто увеличиваем длину отрезка прямой (количество раздражения) в математическом пространстве. Но иногда это бывает необходимо. Функция может быть и другой, можно открыть любой учебник по математике и проникнуться впечатлением, сколько их бывает (и какими они бывают). |
Аналогично и для пространства совершаемой работы. Длина отрезка прямой (количество раздражения) задает длину отрезка прямой (объем совершаемой работы), а координата математической точки относительно раздражителя задает координату точки относительно конечного объема работы, которую нужно совершить (в какую позицию нужно себя переместить). Соответствовать между собой раздражение и совершаемая работа тоже могут по какой угодно функции, хоть в степени. И в этом тоже мало смысла, это просто увеличивает длину отрезка, т.е. это делается только тогда, когда это действительно необходимо.
 |
| Величина раздражения задает величину реакции на раздражение. Не очень удобно считать координаты, потому что начало координат находится справа. Впрочем, мы так и не считаем, предпочитая прибавлять к величине (r). С учетом степени величина реакции на опасность будет запредельной. |
Пусть и через буферное пространство, но величина определения и величина реакции все равно соответствуют друг другу. Чем больше определение, тем выше величина реакции. Со степенями это будет уже не линейная зависимость. Даже если мы переводим разницу температур (или чего-то еще) в величину опасности (какую угрозу для живого существа это несет) один к одному (т.е. линейно), то далее начинаются степени, которые дважды будут ломать линейную зависимость, в результате если незначительная разница температур будет восприниматься живым существом как неопасная (а значит не требующая какой-то запредельной реакции), то значительная разница температур будет восприниматься как опасная (линейно), но вызывать запредельную реакцию (мышечную или какую-то еще). И не только так, мы можем оставить для раздражения и реакции линейную зависимость, но величину опасности определять через степень разницы температур. В этом случае величина опасности будет линейна величине реакции, и незначительная разница температур снова будет восприниматься живым существом как неопасная, реакция тоже будет вялой, но значительная разница температур будет восприниматься как критическая угроза, требующая такой же запредельной реакции.
И все равно может остаться вопрос, зачем нужна математическая реальность, если соответствие (даже нелинейное) можно подобрать и без него. Вопрос справедлив, потому что величины задают размерность другим величинам, не более. Через определение мы задаем не просто команду (инструкцию), но и величину, насколько должны напрячься мышцы живого существа, насколько должен сузиться зрачок, насколько далеко живое существо должно убежать, с какой скоростью, насколько должно увеличиться количество адреналина в крови и так далее. Если увлечься степенями, то даже небольшое раздражение закончится мышечным спазмом, хотя иногда нелинейная зависимость бывает необходима. Но через определение мы не задаем скорость наступления реакции, через какое время и с какой скоростью должны напрячься мышцы до заданной величины, через какое время и с какой скоростью должен сузиться зрачок до заданной величины, через какое время и с какой скоростью живое существо должно убежать далеко, с какой скоростью оно должно увеличивать свою скорость (это называется ускорением, скорость второго порядка) и так далее. Мы понимаем, что критическая угроза требует не только запредельной реакции, но и запредельно быстрой скорости наступления реакции, иначе до заданной величины живое существо банально не доживет.
—
Так как длина отрезка прямой в математической реальности задается как производная от определения, то в качестве внутренних параметров здесь остаются частота вызова определения сознанием (это как проверка изменений во внешней среде, откуда поступают команды (инструкции), так и изменение совершаемой работы с каждым вызовом определения) и параметры возбудимости и сопротивляемости (в зависимости от выбора начала координат, потому что одно соответствует другому, только с другого конца). Чем больше отрезок прямой, тем больше времени нужно точке, чтобы пройти его до конца, но чем быстрее она движется, тем меньше времени нужно, чтобы пройти его до конца, и чем выше частота сознания, тем быстрее пробежит путь точка. Поэтому если важна скорость, то нет смысла делать отрезок прямой в математической реальности слишком длинным, скорее есть смысл удлинять отрезок прямой в пространстве совершаемой работы. Если частота вызовов постоянна, то в качестве переменной может выступать только проводимость (или сопротивляемость), через которые задается скорость движения.
Наше живое существо, даже если оно сделано на микросхеме и из пластика, является материальным телом, поэтому для него справедливо все, что справедливо для физических взаимодействий материальных тел. Другими словами, нам нет необходимости измерять огромные температуры, потому что при высокой разнице значений градусник расплавится, живое существо сломается, сгорит и испарится и так далее. То есть, просто сдохнет. Поэтому для живого существа обычно существует некий приемлемый диапазон входящих определений, дальше которых измерять смысла нет, потому что это конечные для живого существа. Это справедливо для любых входящих параметров, которые подвергаются определению (измерению) как прямо (если явление отражается действительно), так и абстрактно. Если есть некий предельный параметр, за пределами которого живое существо сдохнет, то и абстрактное определение тоже не имеет смыла дальше этого параметра. Если вернуться к нашему примеру, то нет никакого смысла считать угрозой температуру выше предельной, наоборот, любую температуру, близкую к критической, следует считать критическим уровнем опасности. Величина реакции и скорость ее полного наступления должны соответствовать.
 |
| Разница значений (AB) близка к критической (AB max), поэтому и реакция должна быть близка ко мгновенной, нет времени ждать. Это значит, что величина AA' должна быть как можно выше по отношению к полному раздражению AB. При этом величина раздражения AB (длина отрезка прямой) задается величиной определения AB (тоже длина отрезка прямой). Другими словами, степень угрозы высока не только сама по себе, но и относительно максимальной. |
Величина возбудимости может быть константой, ее можно вызвать из памяти, она может и будет производной от обмена веществ и чего-нибудь еще, но нас в своем моделировании интересует чистый случай, где положение точки B(x) относительно точки B(max) задает положение точки A'(m) в математическом пространстве, т.е. ее положение задается внешними условиями (средой). Так как в определении точка является входящей, а в работе исходящей, то в общих чертах AB в определении должно соотноситься с AB max так же, как AA' в раздражении с AB. Длина AA' является величиной возбуждения относительно точки A, если она взята как начало координат, и задается величиной сопротивляемости относительно всего раздражения. Нам даже не обязательно знать, как соотносятся определение и раздражение.
Сопротивляемость = Определение (max) / Определение
Мы помним, что чем ниже сопротивляемость, тем выше порции возбуждения, а значит и скорость проведения возбуждения. В нашем случае разница температур может быть близка к критической (несет угрозу для жизни), а значит критическим является степень угрозы (мы отразили разницу значений абстрактно), поэтому скорость проведения возбуждения и скорость совершаемой работы должны быть максимальны, безотносительно к объему совершаемой работы (эту настройку мы уже обсуждали выше). Т.е., нужно не просто повернуть голову, а сделать это резко, пропорционально уровню угрозы (чем выше, тем быстрее), не просто побежать с какой-то скоростью, а набрать эту скорость как можно быстрее, не просто сузить зрачок на какую-то величину, но и сделать это как можно быстрее. Для нашего примера как можно быстрее набрать заданную частоту вращения пропеллера. Но это с одного конца, а есть второй. Здесь отрезок BB max задает пропорцию для остатка раздражения в каждом акте. Его величину мы можем узнать только через разницу относительно B max, взятой за ноль, поэтому.
Возбудимость = Определение (max) / Определение (max) – Определение
Эффект будет аналогичен, такая мера не задает величины раздражения, а задает скорость проведения возбуждения, поэтому соответствие величин настраивается отдельно, как отдельно задается и величина максимального определения, это еще один внутренний параметр. Мы помним, что возбудимость и сопротивляемость не могут быть равны единице, или быть меньше единицы, потому что тогда возбуждение будет проводиться мгновенно, либо не проводиться вообще, потому что с каждой итерацией скорость будет расти, что приведет к параличу вместо реакции. Они и не могут, потому что даже единица — это соотношение к максимуму как один к одному, не сложно догадаться, что еще на подступах к максимуму живое существо склеит ласты. Но у данного явления есть небольшая коллизия, далеко не всегда максимальное определение привязано именно к смертельной угрозе, это может быть и что-то другое, что не ведет к смерти, но тоже имеет максимум. И вот здесь мы можем наблюдать паралич во всей красе, когда раздражитель есть, и он определяется, но что-то идет не так, какая-то вялость, бездействие, язык присох к горлу и прочие реакции, которые парализованы вместо заданного действия.
—
Величина реакции задается величиной раздражения, а величина раздражения величиной разницы значений (определением), определение привязано к окружающей среде, это исходные условия для расчетов (хотя и не обязательно, если величина вызывается из памяти). Скорость наступления полной реакции задается соотношением определения к максимуму, т.е. тоже окружающей средой, это тоже исходные условия для расчетов (хотя тоже могут вызываться из памяти). Поэтому для каких-то действий с реакцией места вроде бы нет, нужно только задать размерность, как величины раздражения и реакции на раздражение соответствуют друг другу. Но если чешутся руки, то можно вспомнить, что и величина реакции имеет максимум, для нашего примера это максимально возможная частота вращения пропеллера, как максимум выполняемой работы (и больше никак). Какой бы не была величина раздражения, но если она превысила максимально возможную работу, то дальше считать смысла нет. И сердце не может работать с частотой тысячу сокращений с секунду, и мышцы выше определенного напряжения и так далее. Либо просто физически, либо потому что живое существо столько не выдержит и сдохнет.
 |
| Это пример того, что и у реакции на раздражение может быть максимальная величина, выше (или ниже) которой никак. Если считать, что координата (r) — это величина работы при отсутствии раздражения, то координата (k) — это максимальная работа вне зависимости от величины определения и раздражения. |
Если так, то можно привести в соответствие максимумы, но не относительно абсолютного нуля, а относительно установленного положения математической точки на обеих прямых. Например, что максимум определения соотносится с фактическим определением так же, как максимум работы с фактической работой. Получится уравнение с четырьмя неизвестными, но два из них устанавливаются на стадии проектирования (еще до того, как живое существо стало живым), для фактического определения есть контрольно-измерительный прибор (орган чувств), остается только одно неизвестное — фактическая работа.
Определение (max) / Определение = Совершаемая работа (max) / Совершаемая работа
Такое соотношение является наиболее простым (и мы намерено предельно упрощаем) и подразумевает линейность. Что достаточно часто встречается в психологии, как и нелинейность, когда совершаемая работа растет рывком при приближении к максимальному определению. Что тоже достаточно разумно, зачем реагировать на что-то незначительное пропорционально, для нашего примера это было бы нелинейное вращение пропеллера при изменении температуры. Если разница незначительная, то это еще не повод включаться, но при достижении некоторой переломной разницы температур величина скорости вращения будет увеличиваться рывком.
Это снова не имеет никакого отношения к скорости совершаемой работы, просто соответствие величин. Так как такое соотношение задается вменяемо только один раз в проекте разработчика, а далее тиражируется через наследственность, то отклонения от наследственности приводят ко вполне предсказуемым последствиям, в том числе и разным параличам. И если на физиологическом и чувственном уровне такое лечится смертью (с таким отклонением либо не живут, либо живут не долго), то на психологическом, а особенно на социальном уровне, такое не лечится порой вообще. Особенно в интеллектуальной сфере, где максимум интеллектуального напряжения может быть настолько убог, что высокая разница значений выдает на выходе пародию на интеллект, а если разница значений низкая, то даже эту пародию существо будет рожать всю оставшуюся жизнь.
—
Comments