—
This chapter is devoted to the definition of a point in the coordinate space. Any living being exists in a three-dimensional reality, which requires a being to be able to navigate in space, define its position relative to the environment, and position of the environment relative to itself. The coordinate space is not a form of the space of values, but it largely imitates the space of values.
—
The definition of a point in the coordinate space is the distance AB between two points A and B in units of length. Since there can only be one distance between points, both points have the same definition relative to each other (they are at the same distance from each other). Although this is not the only way, but the definition is usually denoted by some digit as the length of a straight line segment (AB). The coordinate space is a digital straight line (measuring scale), that is directed from one point to another in accordance with the rules of analytical geometry.
 |
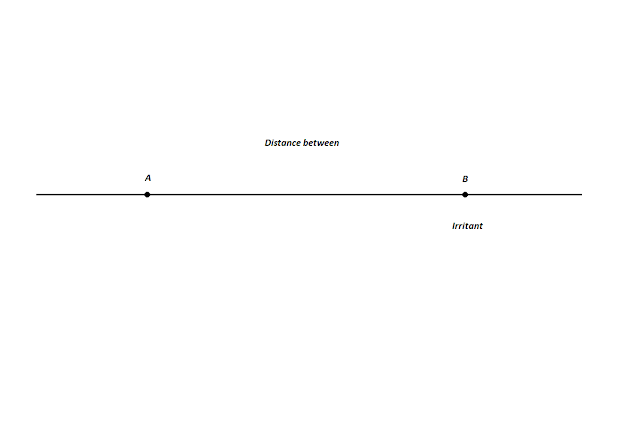| The definition of a point in the coordinate space is the definition of the distance to the irritant in units of length. |
Any living being is quite fragile. It can burn out, get into some other traumatic environment. A living being cannot put out the fire, but it can run away to a safe distance. This is also true for other traumatic factors. In addition, a living being needs to eat something, move somewhere and navigate in space. For all this, need to be able to define distances. In the picture at point A there is a living being, at point B there is the irritant (another living being, some object, etc.). The segment AB is the physical distance between a living being and an irritant, which is measured by the senses and denoted as a digit.
—
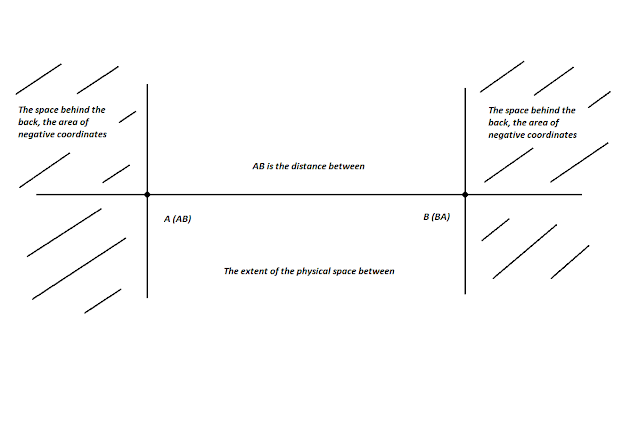
Geometrically, the definition is a straight line segment AB. The rules of geometry tell us, that a straight line can be drawn through two points, and only one. And a straight line segment is a straight line bounded by two points. Accordingly, the definition can be formed only one and only through two points (as the distance between them). By itself, a point is always indefinite (it does not form a straight line segment with itself). This means, that if there is no irritant, then there is no irritation itself. In this case, the point cannot define its location as one of the ends of a straight line segment, because there is no second end of the segment relative to which it can define its position.
 |
| This is a standard mathematical point formation. The distance between is the definition of how different the points are from each other, the quantity of disequilibrium, inconsistency, asymmetry, etc. |
Physically, the definition is a dedicated part of the physical space only in its length (the width and height of the allocated volume are not interesting to psychology). Attracting two points is a method of allocating a part of the physical space by cutting off the space that is outside the two points. The latter lock part of the space inside themselves (among themselves), being the boundaries of the allocated space. In the case of straight lines, this is the selected part of a straight line, where two points are the boundaries of the selected part (the ends of the line segment).
 |
| A part of the physical space in its extent is locked between two points. Beyond the two points, physical space is not interesting, nor is its height and width, only the distance between. Mathematically, the definition is the length of a straight line segment, denoted by a digit. The latter reflects the position (coordinate) of one point relative to another in a one-dimensional coordinate space. To do this, one of the points is placed in the zero position (the origin). Accordingly, the definition is possible only through another point as its coordinate relative to the point at the zero position. Relative to itself, the point will always be indefinite (zero dimension). For distilled psychology, an incoming point is always placed in the zero position. |
 |
| Below is a more familiar option, the distance between the points is a mutual definition, which is indicated by a digit (coordinate). |
Technically, a definition is the result of measuring the distance between two points. Here one of the points (incoming) is the beginning of the reference, the second (outgoing) is the end. The distance between the points becomes a parameter. Since the beginning of the reference cannot coincide with its completion (the zero length of the line segment, which means its absence), the point at the beginning of the reference never has its own parameters. But the parameter, like the distance between points, always has the opposite point. In this case, the incoming and zero point will not have its own dimension and position in space.
—
In theory, there is no need for a coordinate space, if we consider it necessary to regulate a physical parameter. But in practice, a living being is in a physical reality, that has three dimensions. A living being must orient himself in physical reality, be aware of his position relative to the environment, and the position of the environment relative to himself. This is done through distance measurement. If we believe, that a living being should make movement, then this is not just the regulation of velocity and direction of movement, but also awareness of when (under what conditions) it is necessary to adjust the parameters in which direction, as well as control the regulation, how it is adequate to reality. In other words, if we want a living being to eat from a bowl, then we must first teach the living being to define the position of the bowl relative to itself (and its position relative to the bowl), in order to further rotate a living being to the bowl and adjust the velocity so, that the living being comes up and stops. And also to define, how successful it is (it is closer or further away when moving).
 |
| AB is the distance between a living being and something tasty for him. Beyond this distance, the extent is not interesting. There is something delicious at some distance (coordinate (x)) from a living being, and there is a living being at some distance (coordinate (x)) from something delicious. |
Also, the coordinate space is used to extinguish the incoming definition. To do this, the definition of a point in the coordinate space is placed in the denominator, when calculating the quantity of irritation. Thus, the difference in values is extinguished depending on the distance to the source of irritation. The further away the source of irritation, the lower the quantity of irritation.
 |
| The difference in values between a living being and something dangerous is constant, but the irritation, that this difference causes, may decrease with distances. The further away, the less the feeling of fear, that something dangerous causes. |
In theory, the definition of a point in the coordinate space is the distance AB between two points A and B. It is usually customary to denote such a definition in meters, or so. In theory, one of the two points is thought of as the subject, that takes the definition. We call this distance measurement. Accordingly, one of the points is able to measure the distance (it is a control and measuring device or a sense organ) between itself and another point. Any definition in the coordinate space as a result of measurement is always subjective. If we are talking about psychology, then a living being (human or animal) acts as such a point, which subjectively measure the distances between themselves and surrounding points, forming straight lines with them. If there are no points in the environment, then there is no one to form a straight line segment with, then there is no distance, no definition of one’s position and existence. The most elementary definition of a point in the coordinate space will be the logical true or false. Another point, from which can form a straight line segment, is either there or not. The main thing to remember is that a living being is always one of the ends of a straight line segment, this turns a living being (a control and measuring device or a sense organ) into a subject. If a living being measures the distance between two points, then this does not turn it into a subject, only if the living being measures the distance between itself and another point. The irritant is always the second end of a straight line segment. Without this it is impossible to transform the object into a mathematical point.
 |
| If there is no point B (something delicious), then it is impossible to define its position relative to itself (there is the origin of coordinates, but there is no definable point). If point A is outside the line (or absent), then it is impossible to define the position of point B relative to itself (there is a defined point, but there is no origin). Therefore, there is a living being at some distance relative to something tasty, and there is something tasty at some distance relative to a living being. |
We remember about the specific analytical geometry, and we remember about its shortcomings. Therefore, we cannot say, at what distance we are from ourselves. Because it is impossible to form a straight line segment with ourselves (from one point). We also can’t tell, if we are ten meters away from the house, or if the house is ten meters away from us. Because the length of a straight line segment is the same, no matter how we measure, even AB, even BA. We can only define the position difference, by measuring the distance between two points (us and the house). But we can’t say, who exactly owns this difference, us or the house. Because it belongs to two points at the same time. We do not have our own parameters (our own distance relative to ourselves), except for the distance between (our own distance relative to the house), which is our only parameter (or at home, depending on where and where to draw the line, and what to take as the origin). In psychology, other proprietary parameters are not used, only the difference of positions in the form of distance, which is measured (defined) by us subjectively, is important. The width and height of the allocated volume of space between us and the house is also not interested in psychology.
For distilled psychology, the subject always draws a straight line from himself, being an incoming point. The external object, the distance to which need to define (measure), in this case will be the outgoing point. For distilled psychology, the subject is always in the zero position (origin). Accordingly, the external object will have some kind of coordinate relative to the subject. This coordinate will coincide with the length of the line segment. It is always positive, because the directions of a straight line and one-dimensional space always coincide here. Since definitions are always subjective, in practice an error in definition (measurement) is possible. Such errors are commonly called an illusion (distorted measurement of distance) or a hallucination (measurement of distance to a non-existent point). And yes, no one is immune from the error of the measurement itself. Ideal measurements are only possible in theory. Regardless of the result (how adequate it is to reality), the measurement result is called a real definition. This is a certain extent, which we set as a digit, depending on the chosen graduation. The metric can be different, so the same distance can be set in different digits. In addition, the method of defining the distance may also be different (with different control and measuring devices). But in general, the control and measuring device should return the measurement result in the form of some magnitude, that reflects the extent of the space, allocated by two points (real reflection).
—
Then practice breaks in. In theory, points A and B are thought of as geometric. That is, they do not have their own dimension, parameters and other things. This is only a position (coordinate) in physical space. In practice, any bodies have their own geometry, they have dimension. Therefore, the first adjustment of practice to theory is the compression of the body to the state of an abstract geometric point. There are only two options here. This is either the geometric center of the body, which is thought of as the whole body. Or some arbitrary point on the surface of the body (as a rule, this is the point closest to the subject), which is also thought of as the whole body. The output is completely abstract points A and B, under which real objects are hidden. But all subjective definitions (measurements) of distances are made between abstractions. Thus, subjectivity arises already at the first stage, when distances are measured not between real physical objects, but between abstract geometric points that have the property of reflecting real physical objects. Physical reality is transformed into mathematical reality.
In theory, points A and B lie on the same straight line, which is thought of as a one-dimensional space. This is necessary to measure the distance between real bodies, that are compressed to geometric points. In one-dimensional space, points have only one coordinate. In our case, the coordinate of one of the points will be the definition (the distance between the points), the second will have a zero coordinate. However, we live in a three-dimensional world, where a point has three coordinates. Therefore, the next step is to transform a three-dimensional space into a one-dimensional one, which has the following rules.
1. The position of a point in three-dimensional physical space always has the form.
Point (radius, zenith angle, azimuth angle)
Each point has three coordinates in space. They correspond to the concepts of length, width and height. But the width and height are not interesting to us, so the coordinates are set in a spherical coordinate system, where there is a radius (length as the distance between a point and the coordinate center), and two angles.
2. If one of the ends of a straight line segment in three-dimensional physical space has a position.
Point (0, 0, 0)
Then the other end of a straight line segment in three-dimensional physical space always has a position.
Point (radius, 0, 0)
 |
| Point B has three coordinates relative to point A (origin). If we assume that the line on which they both lie sets zero angles, then we can say that point B has only one coordinate relative to point A (the origin of coordinates). |
In a spherical coordinate system, zero angles are set arbitrarily by two rays from the observation point, which is their common origin and the origin of coordinates. If otherwise, then arbitrarily taken points through which two straight lines are formed. Two randomly taken points can coincide in their positions. Thus, zero angles can be specified by just one arbitrary point. Next, we encounter the same technique as in analytic geometry. Why put a point that will set zero angles, if we already have such a point to define? The definition in this case will be the coordinate-radius as the distance between points. And we can neglect the angles, since they will always be the same for both points. If we imagine a sphere, on the surface of which we have applied a point, then we can always form a straight line through a point in the center of the sphere and a point on the surface of the sphere, and assume, that this straight line reflects zero angles for us. Thus, we compress a three-dimensional space into a one-dimensional one.
For distilled psychology, the point in the center of the sphere is always incoming and zero. This is the position of an observer, who subjectively defines (measures) the distance-radius. The point on the surface of the sphere is outgoing, and also has a coordinate, which is the desired definition. In theory, it turns out to be a rather curious moment. We remember, that according to the rules of analytic geometry, both points always look at each other. We remember, that any point on the surface of the sphere lies at zero angles, because it forms a straight line with a point in the center, that reflects the zero angle. Therefore, wherever we put a point on the surface of the sphere, it is always in front of the observer’s eyes in the center, since it is always on the same straight line with him in one-dimensional space. What causes the effect, that the observer sees the entire surface of the sphere right in front of him compressed into a point. We remember, that the observer’s gaze coincides with the direction of the straight line. This means, that the entire volume of the sphere always lies in the area of positive digits. There is no place inside the sphere, where the direction of the straight line and the direction of one-dimensional space are opposite, so the observer has no space behind his back as a area of negative digits. The subject in the center exists in two realities. In the physical, where there are bodies with three coordinates relative to the position of the subject. And in mathematics, where there are only geometric points with one coordinate relative to the position of the subject.
Then practice breaks in again, where it was not possible to withstand the theory, because in practice a point on the surface of a sphere is sometimes in motion and changes its coordinate. We remember, that points exist in one-dimensional space, where they can only approach or move away from each other. Here they have only one coordinate, and one degree of freedom. And in three-dimensional, where they have three coordinates, and three degrees of freedom. Here, a change in the coordinate can be coupled with an objective change in angles or velocities. To solve this problem, the subject in the center of coordinates is given the function of consciousness. Which boils down to the periodic definition of the position of a point, but according to the rules of transformation of three-dimensional space into one-dimensional. This means, that the subject, with a certain frequency per unit of time, redefines the distance to the point, each time drawing a straight line through himself and the defined point, and taking this straight line as new zero angles.
 |
| Point B is moving somewhere. But a living being has consciousness. Consciousness is a regular definition (measurement) with some frequency in time. The old result is reset, the living being produces a new dimension. And so it is constantly, while it is in consciousness (capable of definition per unit of time). |
Thus, the change of the coordinate is fixed primarily in the coordinate space itself — the irritant has become closer or further with each iteration of consciousness.
 |
| Something delicious is moving at the velocity of B’B’’, and also changes the angular coordinates to (f1) and (f2). But this goes past the coordinate space, where only the distance to something tasty is fixed. In particular, something delicious has become closer, than in the last iteration of consciousness. |
The downside of this approach will be the lack of fixing the change in angles and velocities of something delicious. Because with every act of consciousness, the angles are always zero, something delicious is always in front of us on one straight line. But we understand, that objectively something tasty can move towards us, or it can move tangentially. When converting a three-dimensional space into a one-dimensional one, we can only record a change in distance, something tasty has become closer or further away from us, but not angles, which are not present in one-dimensional space. Similarly, for velocities, something tasty can run around us, but in the coordinate space it stands rooted to the spot, because the distance does not change. Velocity and direction of movement are values, for which there is a separate value space. And a living being is able to define these values separately from the distance to the irritant. Is it possible then to consider the lack of fixation through the coordinate space as a minus? No, because if desired, and from the coordinate space, can calculate the velocity and direction. But it’s not just that, we live in a three-dimensional space. If we are faced with the task of adjusting the parameter, then we may not need the coordinate space. But if we have a living being, that needs to navigate in space, then we need a special coordinate space. At least to define whether something tasty (or something dangerous) is closer or further away, than before. Even if we define the velocity and direction of movement of something, it will not give us an answer, where it is relative to us (how far away from us), and where we are relative to this something (how far away from it). Therefore, there is a special coordinate space.
—
There is a definition of the first order — this is a certain distance between points in one act of consciousness. This is, what we talked about above. In the elementary form it is true or false, in the more complex it is a quantity (magnitude). Geometrically, it is a straight line segment bounded by two points, where the positions of two points (a living being and irritant) during interaction are taken as the ends of the straight line segment. Figuratively, we could call it a frame, in which the distance is fixed for some point. However, our life is full of such moments, so…
There is a second-order definition — this is the difference between the current and previous readings. In its elementary form, it is also true or false. True means changing the distance between points. In a more complex case, this is the value, by which the distance between the points has changed. We remember, that in one-dimensional space the distance can only increase or decrease. If the second-order definition returns false or zero, then the distance between the points has not changed. This happens, when moving in parallel, or when rotating one point around another (rotating around a common center). If the second-order definition returns true or some value, then the distance between the points is reduced or increased. We remember the rules of analytical geometry, so we cannot say, which point is in motion (possibly both), and shortens or increases the distance. But we can tell at, what velocity the point is moving (or their sum of velocities), since the velocity here will be the difference in measurements (the distance traveled) per unit of time. This is not the objective velocity of a point in three-dimensional space, but subjective in one-dimensional coordinate space, which way the point passes with each act of consciousness.
 |
| Point B is moving in the coordinate space with some velocity (x'x'') towards us. At what velocity and in what direction it is moving in reality, is also a very interesting question (past us at the velocity of B'B'' and in the direction of f). We can find the answer to this question only if the point is moving towards us or in the opposite direction (angle f = 0). Only in this case the physical velocity and the velocity in the coordinate space will coincide. |
There is a physical velocity, it is a change of position relative to oneself in the past. This is the length of a straight line segment, where the ends are the past and present position of the point. It is equivalent to physical work. And there is a psychological velocity, this is a change of position relative to another point (closer or further, and how much). It is equivalent to psychological work. They can coincide only if the point moves in a straight line, which is formed through the subject and the irritant, in which case the trajectory of movement and the coordinate space coincide as straight lines. Whether they coincide or not, both velocities are separate phenomena. These are two different work in a physical sense. The velocity in the one-dimensional coordinate space can vary, so…
There is a third-order definition — this is the difference between the current and previous second-order definitions. In a simple version, this is true or false, in a complex one, this is the value, by which the definitions of the second order have changed. If the definition returns false or zero, then the distance between the points changes uniformly. This happens, when moving towards (zero angle) and constant velocity. If the definition returns true or some value, then the point is moving at some angle (or both). We remember, that the definition of the second order is velocity as the distance, traveled between two frames, and in one-dimensional space, not three-dimensional. If the path is zero, then the points are fixed relative to each other. Although they can both be in motion relative to the third points. The definition of the third order is the difference in velocities as the paths traveled in three frames, and also in one-dimensional space. This difference is commonly called acceleration or deceleration. If in the three-dimensional world a point flies past another in a straight trajectory without changing velocity, then in the one-dimensional coordinate space it will approach the other slower and slower (going through a smaller path per act), until it stops and starts moving in the opposite direction faster and faster (going through a larger path per act).
 |
| Point B continues to move somewhere past us. Its physical velocity and direction have not changed, but in the coordinate space it continues to approach, although its velocity has decreased by some quantity of deceleration. Then it will stop and start moving away from us in the coordinate space faster and faster, as if it will spring off, until its velocity becomes equal to physical velocity. |
This can be summed up. The difference between theory and practice in the form of a subject (animal or human) is approximately the same, as between thermodynamics and a refrigerator. To put the theory into practice, need to get out somehow, come up with something. To add consciousness as a forced step, to straighten the three-dimensional world into a one-dimensional one, to compress bodies into geometric points. But even this does not help, which is why it is necessary to increase computing power, add memory, which in itself requires structural solutions, and also sets the shape of the structure itself, which should be able to turn around the axis (and even in several variants). And all this is so, that the subject can navigate in three-dimensional space and define distances. We remember, that such subjects are called control and measuring devices, we have a rather complex technique in front of us. And this is not all the complexity.
—
Previous chapter — Analytical geometry
—
Next chapter — Defining a point in the value space
—
Comments